[最も選択された] 場合の数 組み合わせ 220383-場合の数 組み合わせ 高校

Q Tbn And9gcsnd8opqluo Nzq Zgy4t Arez2qauu7f9hrb5h9ibzsstid5n Ay7p Usqp Cau

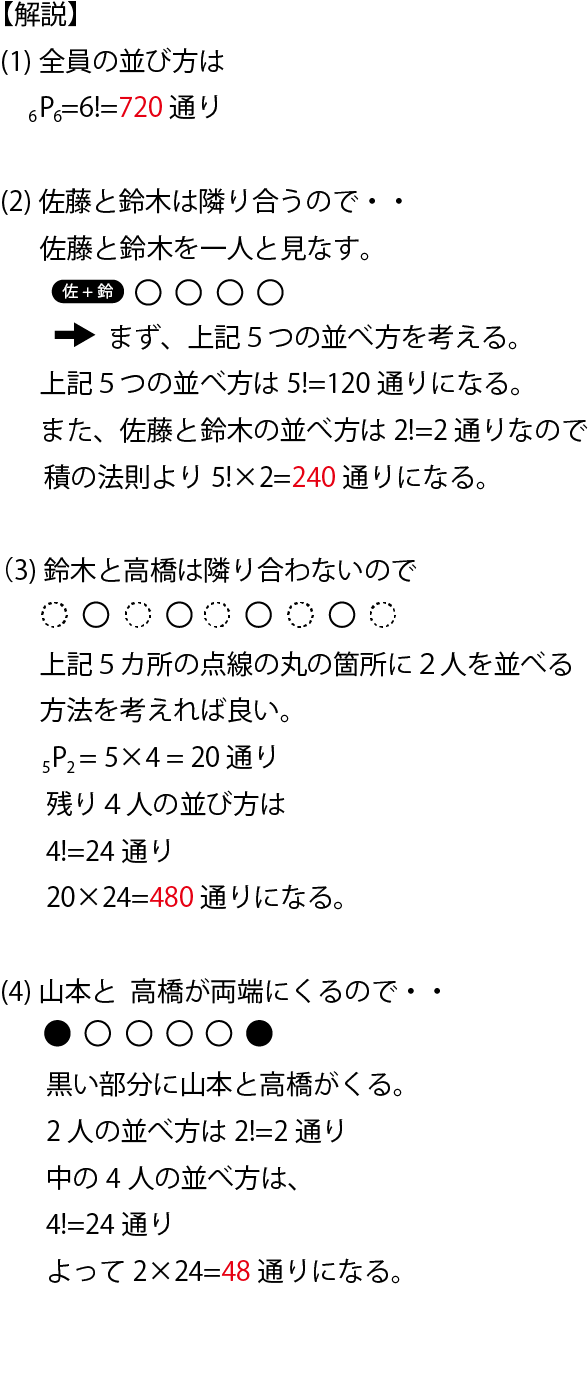
元の数 n n≧r≧0 選ぶ数 r 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁 組合せ数 nCr Combinations (1) nCr =(n r)= n!このように1個多くなってしまった原因は、 集合Aと集合Bに共通して含まれている要素 6 を二重に数えてしまっているからである。 一般に、2つの集合A,Bの要素の個数 n (A) と n (B) を用いて、A

場合の数 組み合わせ 高校

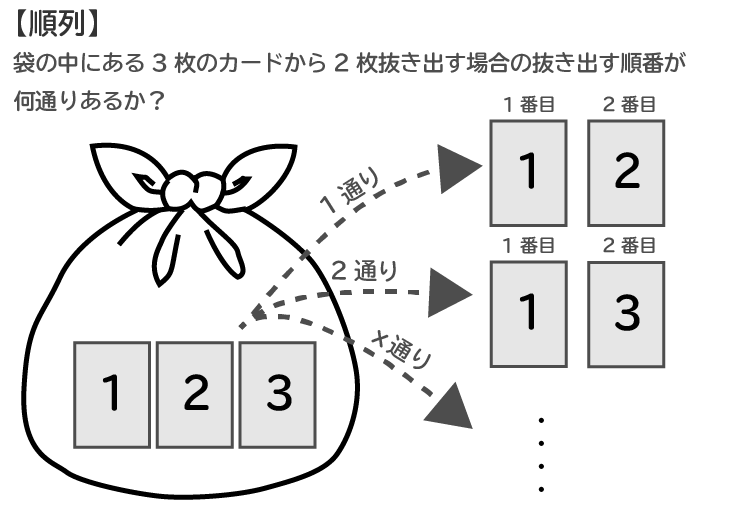
場合の数 組み合わせ 高校- 1問目は順列の場合の数の問題で，2問目は組み合わせの場合の数の問題というわけですね． このように順列の問題と組み合わせの問題を比べると 選んだあとに並べるか 選ぶだけで止め 例えば「A,B,C,D,Eから3文字選ぶ」組み合わせの総数は 5 C 3 と表せる訳です！ ジル 『順列』は並べますが、『組み合わせ』は並べません。 順列の場合は『ABC』と『BAC』は

中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長

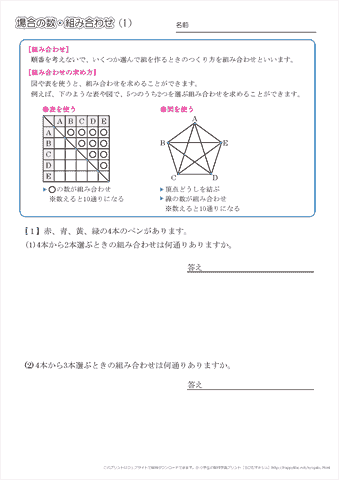
場合の数・順列組み合わせの公式 場合の数の和の法則 A、Bという2つ同時には起こらない事象がある。 Aの起こり方がm通り、Bの起こり方がn通りあるとき、AまたはBの起こる場合の数は、 m＋n組合せ数学 （くみあわせすうがく、 英語 combinatorics ）あるいは 組合せ論 （くみあわせろん）とは、特定の 条件 を満たす（普通は有限の）対象からなる集まりを 研究 する 数学 の 分野 。 離散 場合の数には順列と組み合わせがあります。 ここからは組み合わせの解説です！ 組み合わせは『 順番を考えずに何通り作れますか？ 』という場合の数です。 まあ問題を解きながら理

 組合せの総数 は、C（combinationまたはchooseの頭文字）という記号を使って表されます。 一般に、以下のように定義されています。 組合せの総数 異なる n 個から r 個を選ぶ（取組み合わせ (Combination)とは 組み合わせとは異なるn個の中から異なるr個を取り出す場合の数のことです。 例として、A、B、Cの3つの中から2つを取り出す場合を考えましょう。 書き出してみる(2) nCr = nP r r!

場合の数 組み合わせ 高校のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	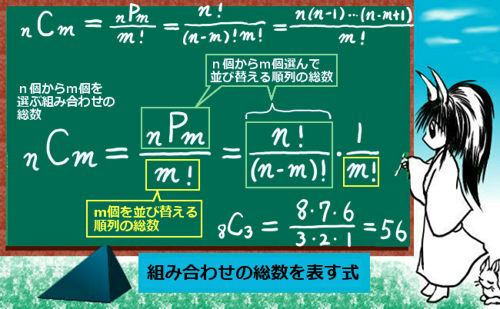場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	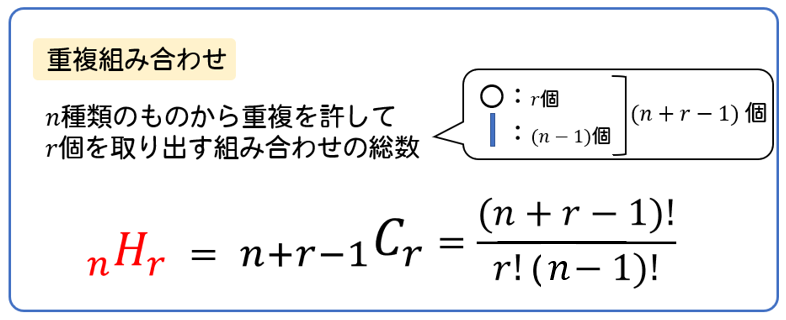場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	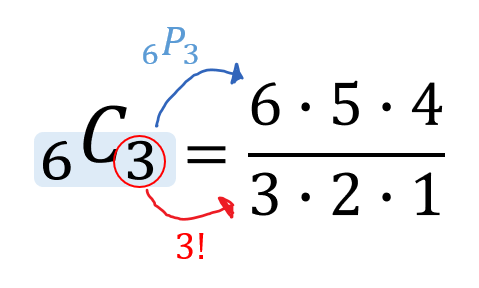場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	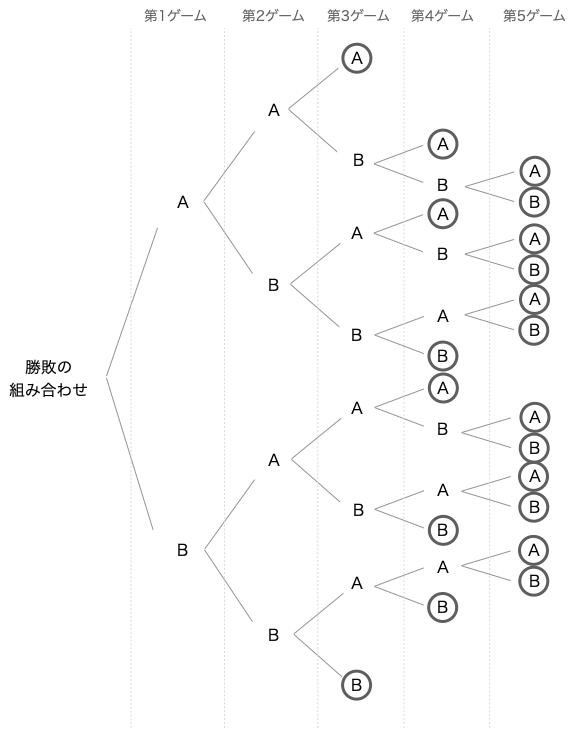場合の数 順列 組み合わせ 久保塾 今治市の学習塾
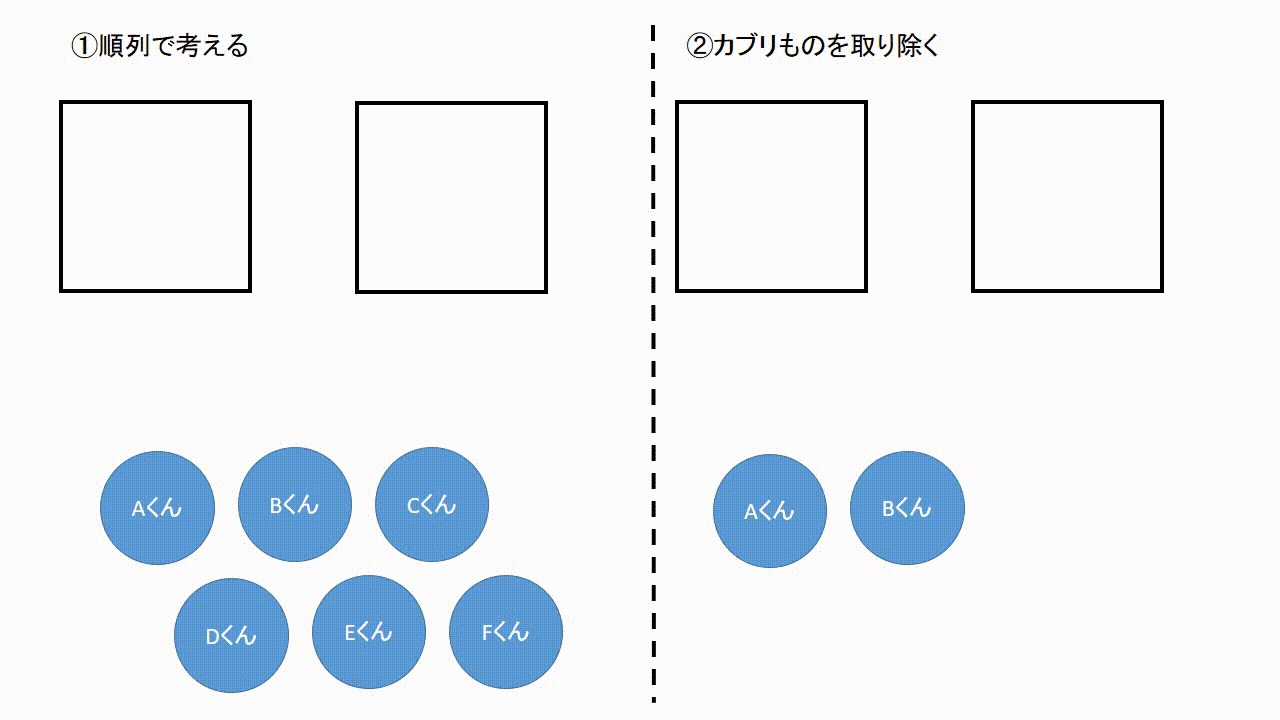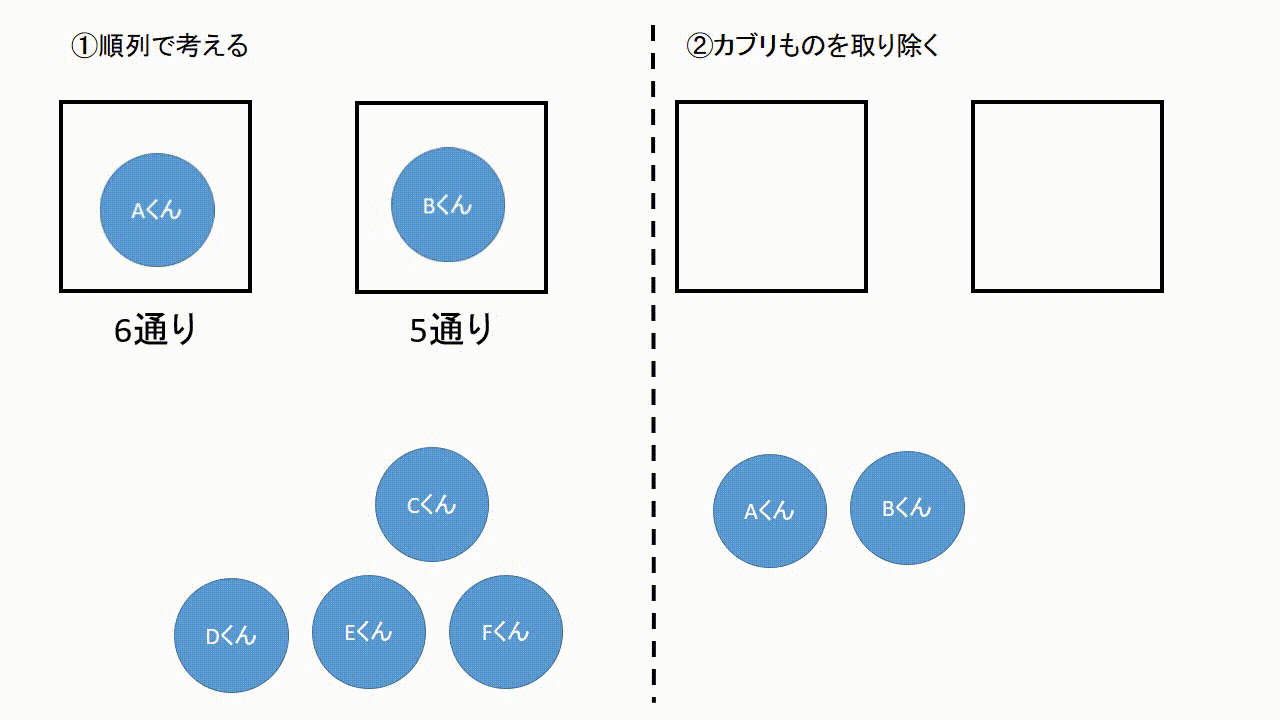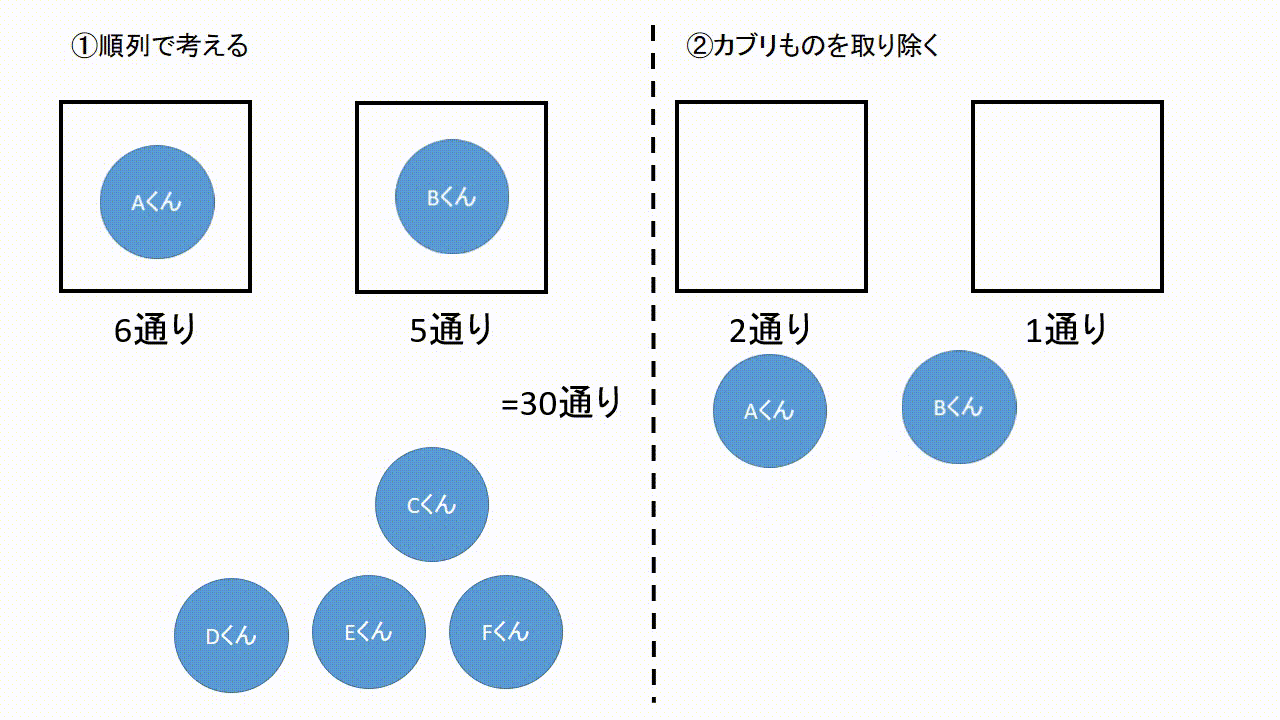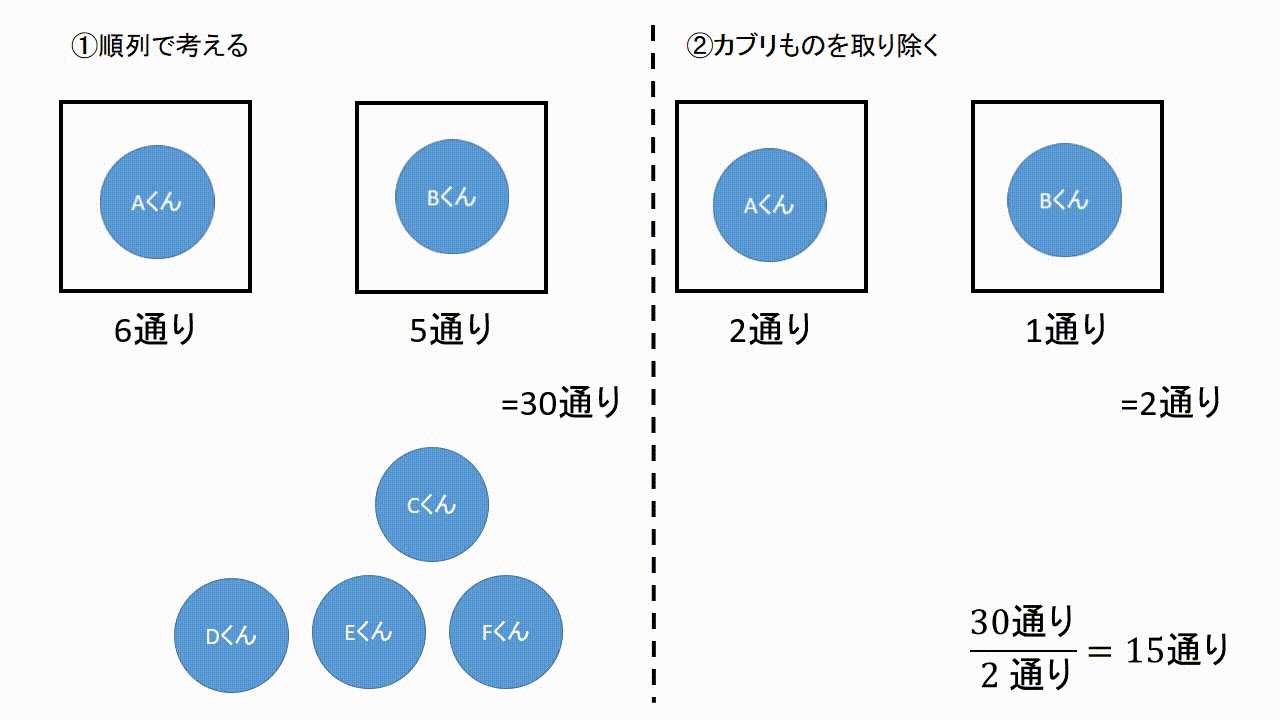場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	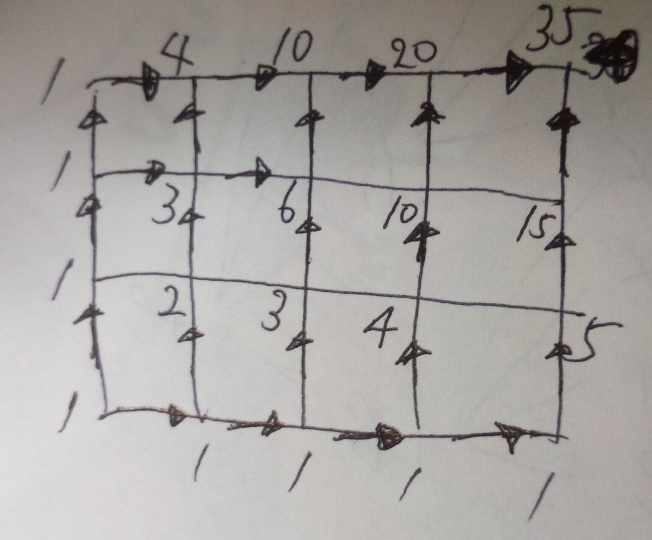場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	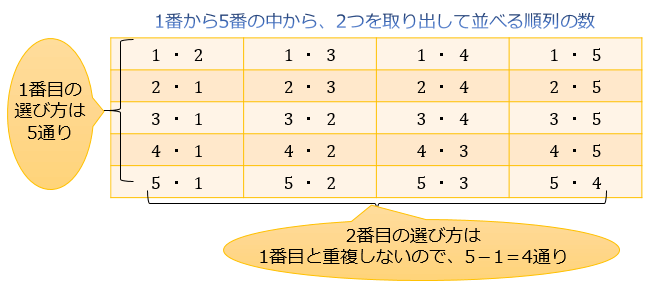場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	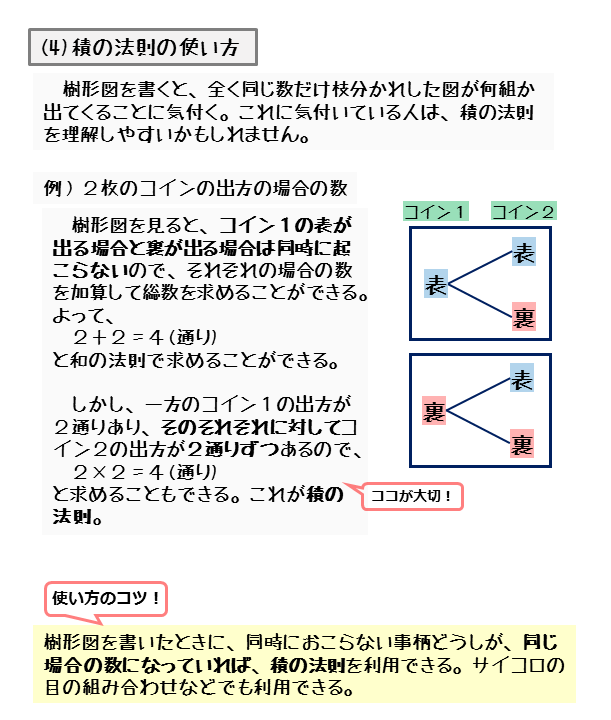場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	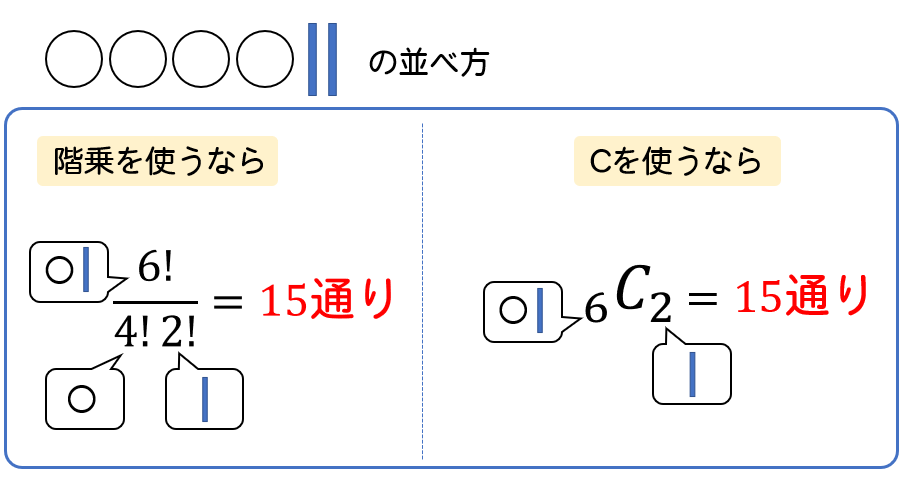場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	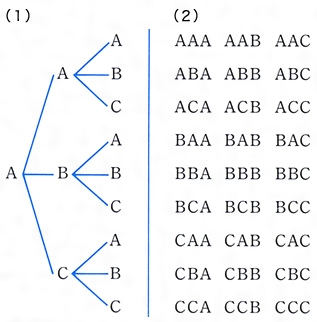場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
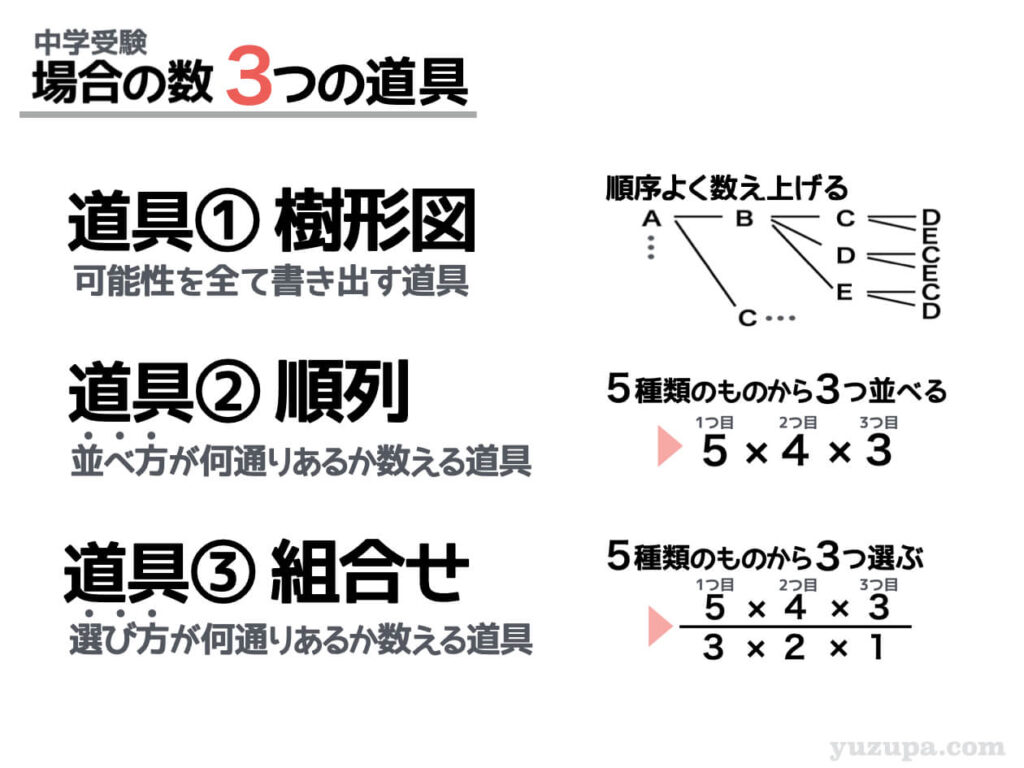場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	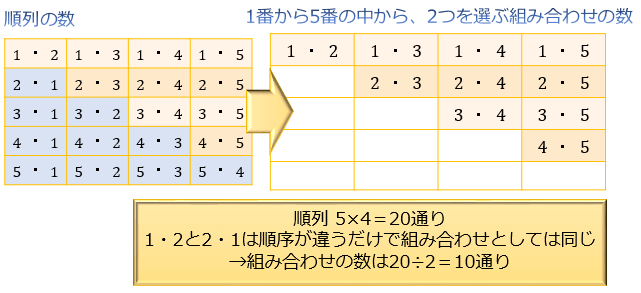場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
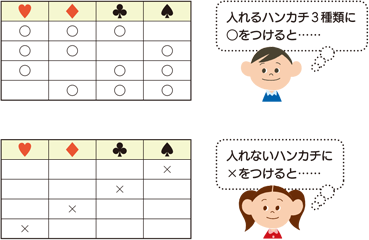場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
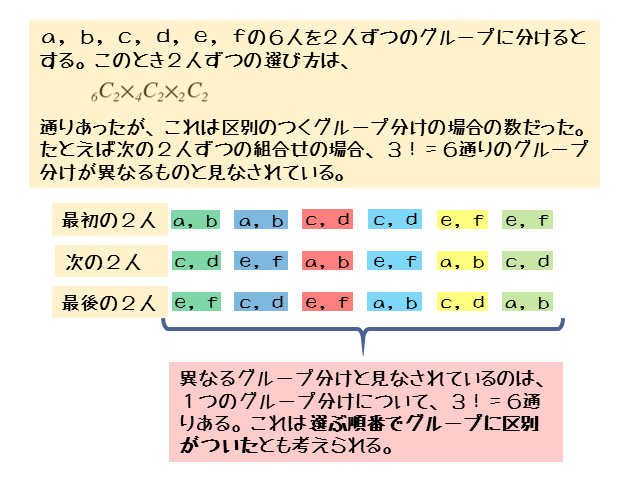場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	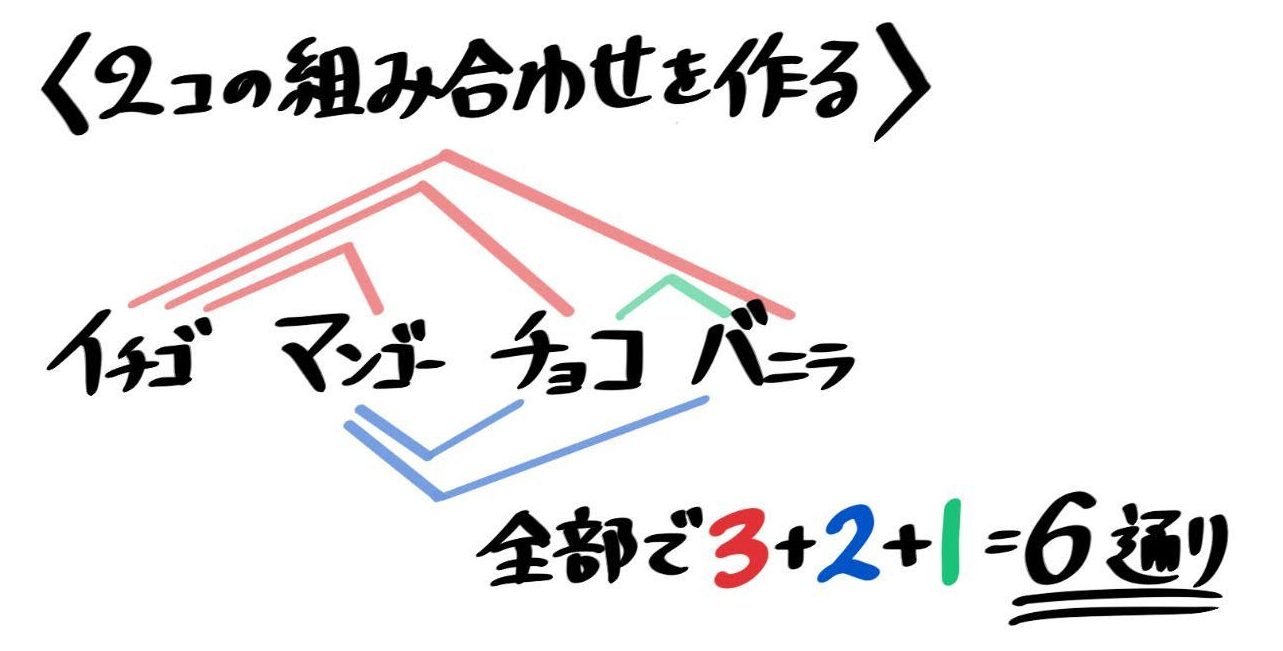場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	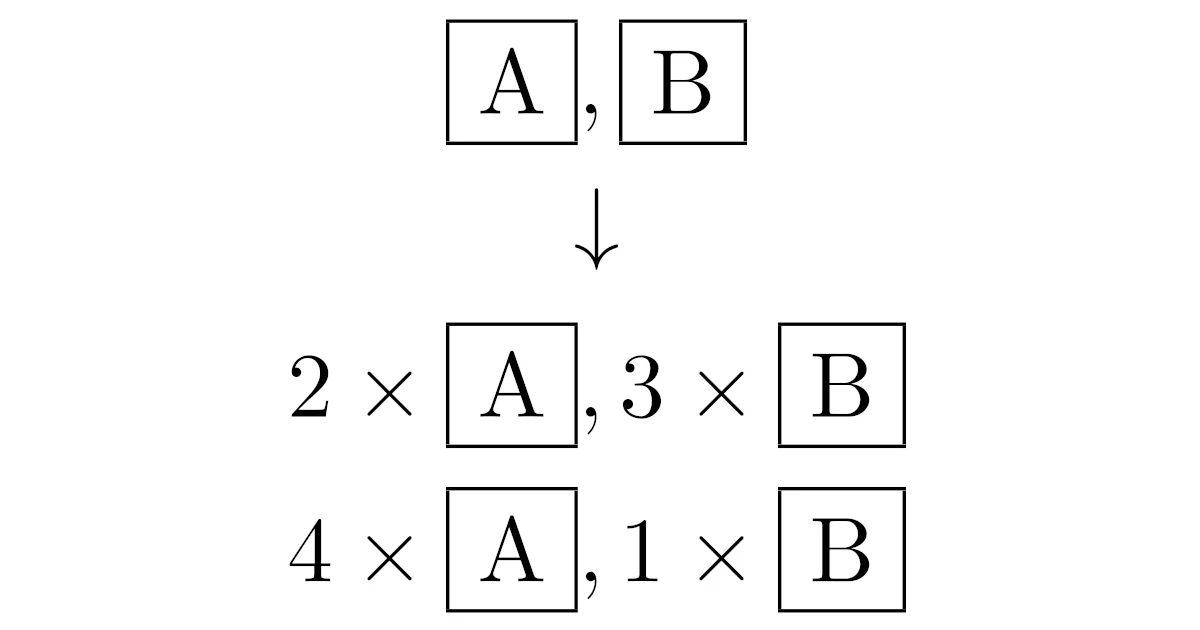場合の数 順列 組み合わせ 久保塾 今治市の学習塾	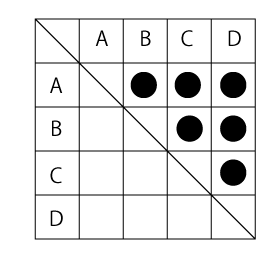場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	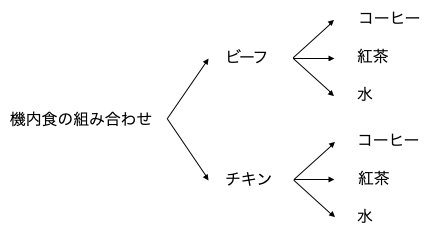場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	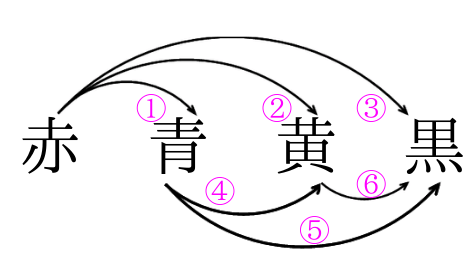場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾
場合の数 順列 組み合わせ 久保塾 今治市の学習塾	場合の数 順列 組み合わせ 久保塾 今治市の学習塾

C o m b i n a t i o n s ( 1) n C r = ( n 組み合わせの総数を求める際には、 並び替えてできるペアをすべて1通りと数え上げ ればOKです。 具体的には、 の計算をすることで求めることができます。 例えば、1, 2, 3, 4枚の

Incoming Term: 場合の数 組み合わせ, 場合の数 組み合わせ 問題, 場合の数 組み合わせ 小6, 場合の数 組み合わせ 公式, 場合の数 組み合わせ 中学受験, 場合の数 組み合わせ 考え方, 場合の数 組み合わせ方, 場合の数 組み合わせ 中学, 場合の数 組み合わせ 小学校, 場合の数 組み合わせ 高校,